ControlledGate
- class ControlledGate[source]
Bases:
ComposedGate,DifferentiableUnitaryAn arbitrary controlled gate.
Given any qudit gate, ControlledGate can add control qudits.
A controlled gate adds arbitrarily controls, and can be generalized for qudit or even mixed-qudit representation.
A controlled gate has a circuit structure as follows:
Where G is the gate being controlled.
To calculate the unitary for a controlled gate, given the unitary of the gate being controlled, we can use the following equation:
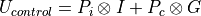
Where
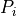 is the projection matrix for the states that don’t
activate the gate,
is the projection matrix for the states that don’t
activate the gate, 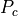 is the projection matrix for the
states that do activate the gate,
is the projection matrix for the
states that do activate the gate, 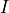 is the identity matrix
of dimension equal to the gate being controlled, and
is the identity matrix
of dimension equal to the gate being controlled, and 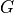 is
the unitary matrix of the gate being controlled.
is
the unitary matrix of the gate being controlled.In the simple case of a normal qubit CNOT,
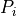 and
and 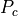 are defined as follows:
are defined as follows: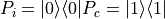
This is because the
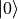 state is the state that doesn’t
activate the gate, and the
state is the state that doesn’t
activate the gate, and the 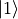 state is the state that
does activate the gate.
state is the state that
does activate the gate.We can also decide to invert this, and have the
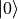 state activate the gate, and the
state activate the gate, and the 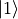 state not activate
the gate. This is equivalent to swapping
state not activate
the gate. This is equivalent to swapping 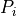 and
and 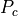 ,
and usually drawn diagrammatically as follows:
,
and usually drawn diagrammatically as follows:When we add more controls the projection matrices become more complex, but the basic idea stays the same: we have a projection matrix for the states that activate the gate, and a projection matrix for the states that don’t activate the gate. As in the case of a toffoli gate, the projection matrices are defined as follows:
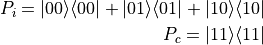
This is because the
 ,
, 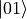 , and
, and
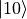 states are the states that don’t activate the
gate, and the
states are the states that don’t activate the
gate, and the 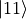 state is the state that does
activate the gate.
state is the state that does
activate the gate.With qudits, we have more states and as such, more complex projection matrices; however, the basic idea is the same. For example, a qutrit controlled-not gate that is activated by the
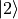 state and not activated by the
state and not activated by the 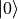 and
and 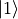 states is defined as follows:
states is defined as follows: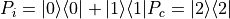
One interesting concept with qudits is that we can have multiple active control levels. For example, a qutrit controlled-not gate that is activated by the
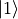 and
and 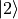 states
and not activated by the
states
and not activated by the 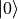 state is defined similarly
as follows:
state is defined similarly
as follows: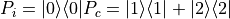
Note that we can always define
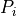 simply from
simply from 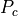 :
: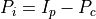
Where
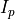 is the identity matrix of dimension equal to the
dimension of the control qudits. This leaves us with out final
equation:
is the identity matrix of dimension equal to the
dimension of the control qudits. This leaves us with out final
equation: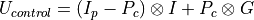
If, G is a unitary-valued function of real parameters, then the gradient of the controlled gate simply discards the constant half of the equation:
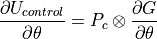
- __init__(gate, num_controls=1, control_radixes=2, control_levels=None)[source]
Construct a ControlledGate.
- Parameters:
gate (
Gate) – The gate to control.num_controls (
int) – The number of controls.control_radixes (
Sequence[int] | int) – The number of levels for each control qudit. If one number is provided, all control qudits will have the same number of levels. Defaults to qubits (2).control_levels (
Sequence[Sequence[int] | int] | int | None) – Sequence of control levels for each control qudit. These levels need to be activated on the corresponding control qudits for the gate to be activated. If more than one level is selected, the subspace spanned by the levels acts as a control subspace. If all levels are selected for a given qudit, the operation is equivalent to the original gate without controls. If None, the highest level acts as the control level for each control qudit. Can be given as a single integer, which will be broadcast as the control level for all control qudits; or as a sequence, where each element describes the control levels for the corresponding control qudit. These can be given as a single integer or a sequence of integers. Defaults to None.
- Raises:
ValueError – If num_controls is less than 1
ValueError – If any control radix is less than 2
ValueError – If any control level is less than 0
ValueError – If the length of control_radixes is not equal to num_controls
ValueError – If the length of control_levels is not equal to num_controls
ValueError – If any control level is repeated in for the same qudit
ValueError – If there exists an i and j where control_levels[i][j] >= control_radixes[i]
Examples
If we didn’t have the CNOTGate we can do it from this gate:
>>> from bqskit.ir.gates import XGate, ControlledGate >>> cnot_gate = ControlledGate(XGate()) >>> cnot_gate.get_unitary() array([[1.+0.j, 0.+0.j, 0.+0.j, 0.+0.j], [0.+0.j, 1.+0.j, 0.+0.j, 0.+0.j], [0.+0.j, 0.+0.j, 0.+0.j, 1.+0.j], [0.+0.j, 0.+0.j, 1.+0.j, 0.+0.j]])
We can invert the controls of a CNOTGate, by activating on the |0> state instead of the |1> state:
>>> from bqskit.ir.gates import XGate, ControlledGate >>> inverted_cnot_gate = ControlledGate(XGate(), control_levels=0)
Also, if we didn’t have the ToffoliGate for qubits, we could do:
>>> from bqskit.ir.gates import XGate, ControlledGate, ToffoliGate >>> toffoli_gate = ControlledGate(XGate(), 2) # 2 controls >>> ToffoliGate().get_unitary() == toffoli_gate.get_unitary() True
We can define a qutrit CNOT that is activated by the |2> state:
>>> from bqskit.ir.gates import ShiftGate, ControlledGate >>> qutrit_x = ShiftGate(3) >>> qutrit_cnot = ControlledGate(qutrit_x, control_radixes=3)
This composed gate can also be used to define mixed-radix controlled systems. For example, we can define a mixed-radix CNOT where the control is a qubit and the X Gate is qutrit:
>>> from bqskit.ir.gates import ShiftGate, ControlledGate >>> qutrit_x = ShiftGate(3) >>> qutrit_cnot = ControlledGate(qutrit_x)
We can also define multiple controls with mixed qudits that require multiple levels to be activated. In this example, The first control is a qutrit with [0,1] control levels, the second qudit is a ququart with a [0] control level, and RY Gate for qubit operation:
>>> from bqskit.ir.gates import RYGate, ControlledGate >>> cgate = ControlledGate( ... RYGate(), ... num_controls=2, ... control_radixes=[3,4], ... control_levels=[[0,1], 0] ... )
Attributes
The matrix dimension for this unitary.
The name of this gate.
The number of real parameters this unitary-valued function takes.
The number of qudits this unitary can act on.
Override default Gate.qasm_name method.
The number of orthogonal states for each qudit.
Control projection matrix determines if the gate should activate.
Identity half of the final unitary equation.
Methods
build_control_proj(control_radixes, ...)Construct the control projection matrix from the control levels.
check_parameters(params)Check parameters are valid and match the unitary.
get_grad([params])Return the gradient for this gate.
Return the gate's inverse as a gate.
get_inverse_params([params])Return the parameters that invert the gate.
get_qasm(params, location)Returns the qasm string for this gate.
Returns a qasm gate definition block for this gate.
get_unitary([params])Return the unitary for this gate, see
Unitaryfor more.get_unitary_and_grad([params])Return the unitary and gradient for this gate.
Return true if this unitary doesn't take parameters.
Check if all sub gates are differentiable.
Check if all sub gates are locally optimizable.
Return true if this unitary is parameterized.
Return true if this unitary can only act on qubits.
is_qudit_only(radix)Return true if this unitary can only act on radix-qudits.
Return true if this unitary can only act on qutrits.
is_self_inverse([params])Checks whether the unitary is its own inverse.
with_all_frozen_params(params)Freeze all of a gate's parameters so they don't change from optimization.
with_frozen_params(frozen_params)Freeze some of a gate's parameters so they don't change from optimization.